謝銘倫Ming-Lun Hsieh

中央研究院數學研究所研究員

研究p 進L 函數的構成 發展在橢圓曲線算術的應用

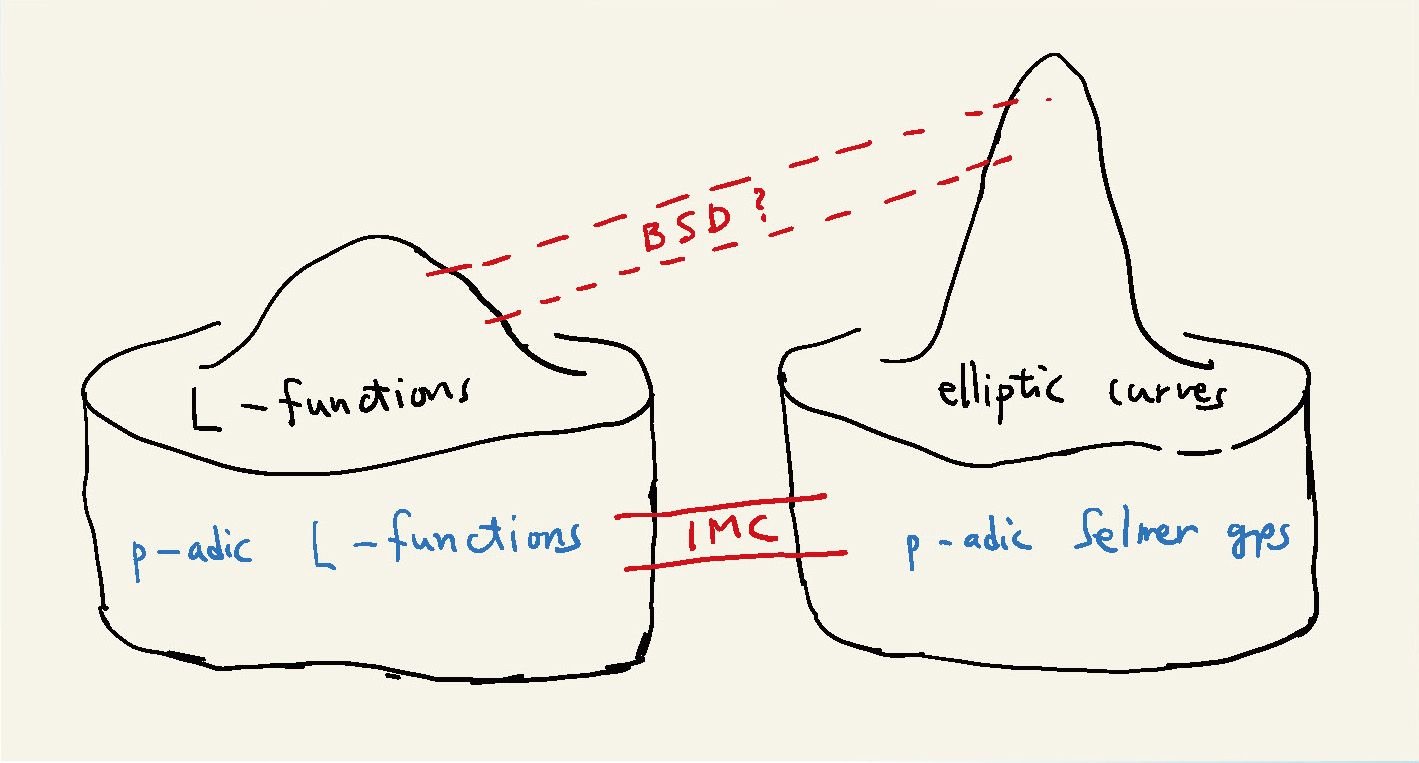
My current research focuses on the construction of p-adic L-functions and their arithmetic applications to elliptic curves. In particular, my works are closely connected with one of the famous 7 millennium problems in mathematics: the Brich and Swinnerton-Dyer conjecture. This conjecture asserts the equality of two distinct invariants associated with elliptic curves over the rational number field: the Mordell-Weil rank and the analytic rank. This conjecture is largely known in the special cases where the analytic rank is not greater than 2. The method in these special cases relies crucially on the existence of Heegner points of elliptic curves. Therefore,it has been an important problem for number theorists to figure out the analogues of Heegner points in higher r ank case.


In 2016, Darmon and Rotger constructed generalized Kato classes for elliptic curves and conjectured that these classes are non-vanishing precisely when the rank of elliptic curves is two.


In my recent work, I obtained the explicit formulae for p-adic L-functions associated with a triple product of p-adic families of elliptic newforms of slope zero, and obtain the factorization formula for the p-adic triple product L-functions associated with elliptic curves over imaginary quadratic fields. With this formula, Castella and I verified partially the conjecture of Darmon and Rotger. This may shed some light on the search of the analogues of Heegner points for rank two elliptic cur ves.

得獎感言

非常榮幸能夠獲獎。我在2015 年後改變研究主題，從研究Eisenstein 級數的同餘方法到Euler系統與p- 進L 函數的構造的相關問題。對於新主題5 年來的工作成果來說，這次獲獎是很大的肯定。非常謝謝我的家人、中研院數學所的同事，以及國家科學理論中心數學組的同仁們，謝謝你們這些年來對我的的協助與支持。

個人勵志銘

Few, but ripe.