艾沃克 Volker Elling

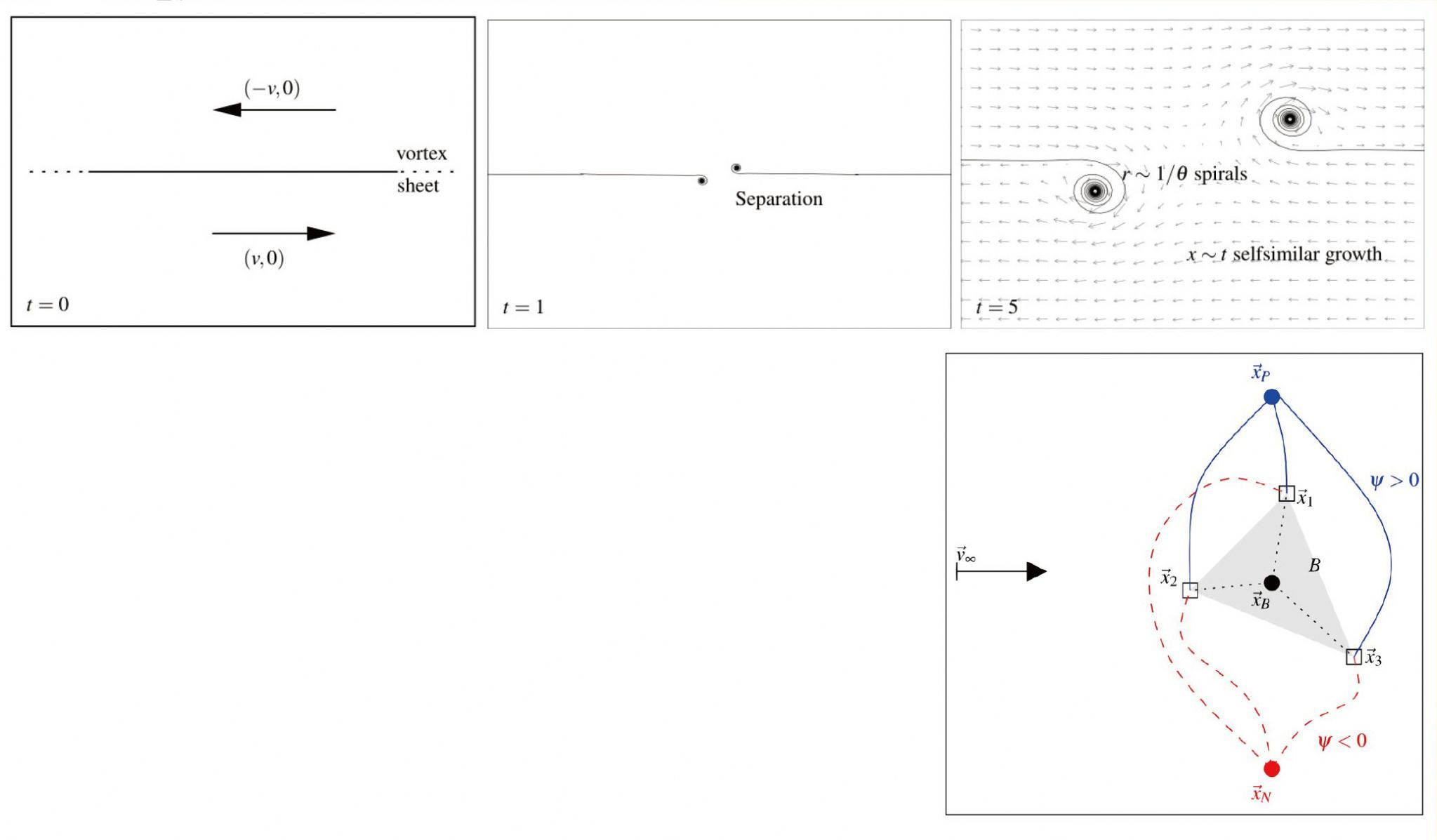
研究流體力學 證明代數渦旋螺旋 (algebraic vortex spirals) 的存在

Flow of fluids is an important subject throughout science and engineering. The two most important models are the Euler and the Navier-Stokes equations. The availability of fast computers has permitted the simulation of complex flows, but the reliability of the results is currently unclear. Differences between models or computer prediction and reality can have costly or catastrophic consequences.

In recent years it has become increasingly clear, in part due to my own work, that the Euler equations permit multiple solutions forward in time for a single set of initial data. This phenomenon appears to require non-smooth flow features such as shock waves or vortex sheets, which are commonly observed.

There is a gap between computer-generated non-uniqueness examples that do not have a rigorous proof, and abstract examples that do have a proof but are not clearly physical flows. The former leave uncertainty, the latter allow hope that some additional admissiblity conditions can select one of several solutions. My research aims to close the gap and give a rigorous proof of a clearly physical flow. I have succeeded in constructing the first cases of algebraic vortex spirals, and I am working on proving non-uniqueness examples using such spirals.

In separate ongoing work I am trying to simplify the possible examples beyond spirals. I have also shown that creation of vortex sheets is inevitable at sharp corners of solids, in some cases proving that no nonvortical solutions can exist. In earlier work I found that the non-uniqueness phenomenon has already appeared in computer calculations, in the guise of the so-called carbuncle phenomenon.